SUMA Y RESTA DE POLINOMIOS

Antes de empezar a explicar como sumar y estar polinomios debemos tener muy claro qué son los términos de un polinomio.

Un término se compone de:

• Un número (si no aparece ninguno es que tiene un 1)
• Una o más variables, que pueden estar elevadas a algún exponente o no.

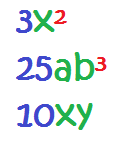
Los diferenciamos porque están separados por los signos de suma y resta en el polinomio.

Un polinomio de un solo término se llama monomio, con dos términos se llama binomio y con tres términos trinomio.

Términos Semejantes

¿Qué son los términos semejantes? Los términos semejantes son aquellos que tienen las mismas variables elevadas a los mismos exponentes y esto último es muy importante, ya que si hay un pequeño cambio, ya no serían términos semejantes y no podrían sumarse o restarse.

Los términos de cada línea son semejantes entre sí:

Pero estos dos términos no son semejantes:

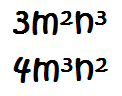
Estos dos términos parecen semejantes pero no lo son, ya que las variables m y n no están elevados al mismo exponente (aunque lo parece, si vamos con prisa y no nos damos cuenta de que no son iguales)

Cómo Sumar y Restar Polinomios

Cuando se aprende a sumar y restar números, te enseñan que se suman las manzanas con las manzanas y las naranjas con las naranjas.

Para sumar y restar polinomios ocurre algo parecido, ya que debes tener en cuenta de que sólo se pueden sumar términos semejantes, es decir, como hemos indicado antes, los términos con las mismas variables y elevadas al mismo exponente.

Realmente, cuando sumamos y restamos números (naturales o enteros), son también términos semejantes, donde cada término no tiene variables.

Entonces, para sumar o restar los términos semejantes, se siguen los siguientes pasos:

1. Se suma o resta el número que tenga delante.

2. Se mantienen las variables con sus exponentes.

Suma  de Polinomios de dos Términos

Vamos a resolver un sencillo ejemplo de sumar y restar polinomios de tos términos (binomios), paso a paso:

a² + 3a² =

Tenemos dos términos: a² y 3a²

En el término a² tenemos:

• Número: 1 (cuando no lleva nada es que tiene un 1)
• Variables con sus exponentes: a²

En el término 3a² tenemos:

• Número: 3
• Variables con sus exponentes: a²

En ambos términos, las variables con sus exponentes son a², son exactamente iguales, es decir, son términos semejantes. Por tanto, se pueden sumar y restar:

1. Se suman o restan los números: 1 + 3 = 4
2. Las variables se mantienen: a²

a² + 3a²= 4a²

Estos pasos, cuando se tiene más práctica se hacen de memoria, pero para entenderlos lo indicamos así, poco a poco.

Vamos a ver otro ejemplo muy similar al anterior, pero con una pequeña diferencia:

a² + 3a³ =

Tenemos dos términos: a² y 3a³

En el término a² tenemos:

• Número: 1 (cuando no lleva nada es que tiene un 1)
• Variables con sus exponentes: a²

En el término 3a³ tenemos:

• Número: 3
• Variables con sus exponentes: 3a³

Ahora las variables coinciden, pero no sus exponentes, ya que uno está elevado al cuadrado y el otro al cubo.

Estos términos no se pueden sumar porque no son semejantes.

Resta de Polinomios

En ocasiones, nos piden sumar y restar polinomios, pero nos dan cada uno de ellos por separado.

Por ejemplo: Sumar y restar los siguiente polinomios:

P(x) = 2x² – 5x + 3

Q(x) = x² + 2x – 4

Para sumarlos, no tiene mayor dificultad:

P(x) + Q(x) =

= (2x² – 5x + 3) + (x² + 2x – 4) =

Siguiendo la jerarquía de operaciones, eliminamos paréntesis:

= 2x² – 5x + 3 + x² + 2x – 4 =

Ahora sumamos y restamos cada uno de los términos semejantes por separado:

• 2x² + x² = 3x²
• -5x + 2x = -3x
• 3 – 4 = -1

= 3x² – 3x – 1

Ahora vamos con la resta:

P(x) – Q(x) =

= (2x² – 5x + 3) – (x² + 2x – 4) =

Ahora al eliminar los paréntesis, tenemos en cuenta que el signo menos cambia de signo al contenido del paréntesis que tiene detrás, ya que es equivalente a multiplicar por -1:

= 2x² – 5x + 3 – x² – 2x + 4 =

Ahora sumamos y restamos cada uno de los términos semejantes por separado, igual que en el caso anterior:

• 2x² – x² = x²
• -5x – 2x = -7x
• 3 + 4 = 7

= x² – 7x + 7

Como conclusión, sumar y restar polinomios, es como sumar y restar números enteros, a los que le añadimos las variables y teniendo en cuenta que sólo se pueden sumar y restar términos semejantes.