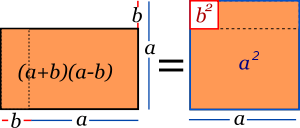
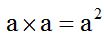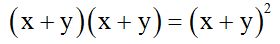Binomio de suma al cubo

Un binomio al cubo (suma) es igual al cubo del primero

 más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.

(a + b)³ = a³ + 3 · a² · b + 3 · a · b² + b³

(x + 3)³ = x ³ + 3 · x² · 3 + 3 · x· 3² + 3³ =

= x³ + 9x² + 27x + 27

Binomio de resta al cubo

Un binomio al cubo (resta) es igual al cubo del primero 
menos el triple del cuadrado del primero por el segundo más el triple del primero por el cuadrado del segundo, menos el cubo del segundo.

(a − b)³ = a³ − 3 · a² · b + 3 · a · b² − b³

(2x − 3)³ = (2x)³ − 3 · (2x)² ·3 + 3 · 2x· 3² − 3³ =

= 8x ³ − 36 x² + 54 x − 27

Ejemplos

1(x + 2)³ = x³ + 3 · x² · 2 + 3 · x · 2² + 2³ =

= x³ + 6x² + 12x + 8

2(3x − 2)³ = (3x)³ − 3 · (3x)² · 2 + 3 · 3x · 2² − 2³ =

= 27x ³ − 54x² + 36x − 8

3(2x + 5)³ = (2x)³ + 3 · (2x)² ·5 + 3 · 2x · 5² + 5³ =

= 8x³ + 60 x² + 150 x + 125

Producto de binomios con término común[editar]

Dos binomios con un término común[editar]

Ilustración gráfica del producto de binomios con un término común.

Para efectuar un producto de dos binomios con término común se tiene que identificar el término común, en este caso x, luego se aplica la fórmula siguiente:

${\displaystyle (x+a)(x+b)=x^{2}+(a+b)x+ab\,}$

Ejemplo:

${\displaystyle (2y-1)(2y-3)=(2y)^{2}+(-1-3)(2y)+((-1)(-3))=4y^{2}-8y+3}$

Tres binomios con término común

Fórmula general:

${\displaystyle (x+a)(x+b)(x+c)=x^{3}+(a+b+c)x^{2}+(ab+ca+cb)x+abc}$

Binomios con término común

Fórmula general:

${\displaystyle (x+a_{1})\cdot \dots \cdot (x+a_{n})=x^{n}+(a_{1}+\dots +a_{n})x^{n-1}+((a_{1}a_{2}+a_{1}a_{3}+\dots a_{1}a_{n})+(a_{2}a_{3}+\dots +a_{2}a_{n})+\dots +(a_{n-1}a_{n}))x^{n-2}+\dots (a_{1}\cdot \dots \cdot a_{n})}$

xⁿ + (suma de términos no comunes agrupados de uno en uno)x^n-1 + (suma de términos no comunes agrupados de dos en dos)x^n-2 +… + (producto del número de términos)

Producto de dos binomios conjugados[ed

Producto de binomios conjugados.

Dos binomios conjugados se diferencian solo en el signo de la operación. Para su multiplicación basta elevar los monomios al cuadrado y restarlos (obviamente, un término conserva el signo negativo), con lo cual se obtiene una diferencia de cuadrados.

${\displaystyle (a+b)(a-b)=a^{2}-b^{2}\,}$

Ejemplo:

${\displaystyle (3x+5y)(3x-5y)=\,}$

${\displaystyle (3x)(3x)+(3x)(-5y)+(5y)(3x)+(5y)(-5y)\,}$

Agrupando términos:

${\displaystyle (3x+5y)(3x-5y)=9x^{2}-25y^{2}\,}$

A este producto notable también se le conoce como suma por la diferencia.

• En el caso ${\displaystyle (p-a+b+c)=(p-a-b-c)=(p-a)^{2}-(b+c)^{2}}$,^{n 1} aparecen polinomios.

Cuadrado de un polinomio[editar]

Elevación de un trinomio al cuadrado de forma gráfica.

Para elevar un polinomio de cualquier cantidad de términos se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.

${\displaystyle (a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(ab+ac+bc)\,}$

${\displaystyle (a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(ab+ac+ad+bc+bd+cd)\,}$

Ejemplo:

${\displaystyle (3x+2y-5z)^{2}=(3x+2y-5z)(3x+2y-5z)\,}$

Multiplicando los monomios:

${\displaystyle (3x+2y-5z)^{2}=3x\cdot 3x+3x\cdot 2y+3x\cdot (-5z)\,}$

${\displaystyle +2y\cdot 3x+2y\cdot 2y+2y\cdot (-5z)\,}$

${\displaystyle +(-5z)\cdot 3x+(-5z)\cdot 2y+(-5z)\cdot (-5z)\,}$

Agrupando términos:

${\displaystyle (3x+2y-5z)^{2}=9x^{2}+4y^{2}+25z^{2}+2(6xy-15xz-10yz)\,}$

Luego:

${\displaystyle (3x+2y-5z)^{2}=9x^{2}+4y^{2}+25z^{2}+12xy-30xz-20yz\,}$

Romper moldes

${\displaystyle x(x+1)(x+2)(x+3)+1=(x^{2}+3x+1)^{2}}$.^{n 2}

PRODUCTOS NOTABLES

Son productos cuyo resultado se obtiene sin necesidad de efectuar la operación de multiplicar siendo suficiente aprenderse de memoria su desarrollo clásico.
Antes de comenzar a estudiarlos recordamos que para multiplicar términos semejantes se suman los exponentes:

Los factores pueden ser binomios:

Cada factor ( X + Y ) es una potencia de base ( X + Y ) y su exponente es 1. Para multiplicar ambos factores, se suman los exponentes.

SUMA Y RESTA COMBINADA

1- ¿Qué son las operaciones combinadas?

Las operaciones combinadas son aquellas en las que aparecen varias operaciones aritméticas para resolver. Debes considerar que para obtener el resultado correcto debes seguir las siguientes reglas:

2- Separar los términos y luego resolver cada uno de ellos.

- Se resuelven las operaciones encerradas entre paréntesis, corchetes y llaves.
- Las operaciones entre paréntesis (         ) son las primeras que se deben resolver.
- Una vez resueltas las operaciones entre paréntsis, se resuelven las que se encuentran dentro de los corchetes  [            ] .
- Una vez resueltas las operaciones entre corchetes, se resuelven las que se encuentran dentro de las llaves {           }.

1.2- Si un ejercicio presenta adición y sustracción, debemos resolver las operaciones en el orden que se presentan, comenzando desde la izquierda.

Analicemos el siguiente ejemplo:  

 

Como la sustracción va primero, obtenemos la resta, que en este caso es 1740. Luego , la anotamos debajo y, después, le sumamos los 5.234. El resultado final es 6.974.

En el caso que la adición estuviera en primer lugar, quedaría:

Primero resolvemos la adición y a la suma obtenida le restamos 1.348. El resultado final es 4.807.

3- Cuando hay paréntesis, los debemos resolver en primer lugar.

Analicemos el siguiente ejemplo:

Como puedes ver, los paréntesis se resuelven en el orden que aparecen de izquierda a derecha. Se pone el resultado de las operaciones, que van dentro de ellos, debajo de cada uno. Luego, se obtiene la suma que está a la izquierda. Para terminar, restamos su resultado con el número final.

SUMA Y RESTA DE POLINOMIOS

Antes de empezar a explicar como sumar y estar polinomios debemos tener muy claro qué son los términos de un polinomio.

Un término se compone de:

• Un número (si no aparece ninguno es que tiene un 1)
• Una o más variables, que pueden estar elevadas a algún exponente o no.

Los diferenciamos porque están separados por los signos de suma y resta en el polinomio.

Un polinomio de un solo término se llama monomio, con dos términos se llama binomio y con tres términos trinomio.

Términos Semejantes

¿Qué son los términos semejantes? Los términos semejantes son aquellos que tienen las mismas variables elevadas a los mismos exponentes y esto último es muy importante, ya que si hay un pequeño cambio, ya no serían términos semejantes y no podrían sumarse o restarse.

Los términos de cada línea son semejantes entre sí:

Pero estos dos términos no son semejantes:

Estos dos términos parecen semejantes pero no lo son, ya que las variables m y n no están elevados al mismo exponente (aunque lo parece, si vamos con prisa y no nos damos cuenta de que no son iguales)

Cómo Sumar y Restar Polinomios

Cuando se aprende a sumar y restar números, te enseñan que se suman las manzanas con las manzanas y las naranjas con las naranjas.

Para sumar y restar polinomios ocurre algo parecido, ya que debes tener en cuenta de que sólo se pueden sumar términos semejantes, es decir, como hemos indicado antes, los términos con las mismas variables y elevadas al mismo exponente.

Realmente, cuando sumamos y restamos números (naturales o enteros), son también términos semejantes, donde cada término no tiene variables.

Entonces, para sumar o restar los términos semejantes, se siguen los siguientes pasos:

1. Se suma o resta el número que tenga delante.

2. Se mantienen las variables con sus exponentes.

Suma  de Polinomios de dos Términos

Vamos a resolver un sencillo ejemplo de sumar y restar polinomios de tos términos (binomios), paso a paso:

a² + 3a² =

Tenemos dos términos: a² y 3a²

En el término a² tenemos:

• Número: 1 (cuando no lleva nada es que tiene un 1)
• Variables con sus exponentes: a²

En el término 3a² tenemos:

• Número: 3
• Variables con sus exponentes: a²

En ambos términos, las variables con sus exponentes son a², son exactamente iguales, es decir, son términos semejantes. Por tanto, se pueden sumar y restar:

1. Se suman o restan los números: 1 + 3 = 4
2. Las variables se mantienen: a²

a² + 3a²= 4a²

Estos pasos, cuando se tiene más práctica se hacen de memoria, pero para entenderlos lo indicamos así, poco a poco.

Vamos a ver otro ejemplo muy similar al anterior, pero con una pequeña diferencia:

a² + 3a³ =

Tenemos dos términos: a² y 3a³

En el término a² tenemos:

• Número: 1 (cuando no lleva nada es que tiene un 1)
• Variables con sus exponentes: a²

En el término 3a³ tenemos:

• Número: 3
• Variables con sus exponentes: 3a³

Ahora las variables coinciden, pero no sus exponentes, ya que uno está elevado al cuadrado y el otro al cubo.

Estos términos no se pueden sumar porque no son semejantes.

Resta de Polinomios

En ocasiones, nos piden sumar y restar polinomios, pero nos dan cada uno de ellos por separado.

Por ejemplo: Sumar y restar los siguiente polinomios:

P(x) = 2x² – 5x + 3

Q(x) = x² + 2x – 4

Para sumarlos, no tiene mayor dificultad:

P(x) + Q(x) =

= (2x² – 5x + 3) + (x² + 2x – 4) =

Siguiendo la jerarquía de operaciones, eliminamos paréntesis:

= 2x² – 5x + 3 + x² + 2x – 4 =

Ahora sumamos y restamos cada uno de los términos semejantes por separado:

• 2x² + x² = 3x²
• -5x + 2x = -3x
• 3 – 4 = -1

= 3x² – 3x – 1

Ahora vamos con la resta:

P(x) – Q(x) =

= (2x² – 5x + 3) – (x² + 2x – 4) =

Ahora al eliminar los paréntesis, tenemos en cuenta que el signo menos cambia de signo al contenido del paréntesis que tiene detrás, ya que es equivalente a multiplicar por -1:

= 2x² – 5x + 3 – x² – 2x + 4 =

Ahora sumamos y restamos cada uno de los términos semejantes por separado, igual que en el caso anterior:

• 2x² – x² = x²
• -5x – 2x = -7x
• 3 + 4 = 7

= x² – 7x + 7

Como conclusión, sumar y restar polinomios, es como sumar y restar números enteros, a los que le añadimos las variables y teniendo en cuenta que sólo se pueden sumar y restar términos semejantes.

REDUCCIÓN DE TERMINOS

En una expresión algebraica se llaman términos semejantes a todos aquellos términos que tienen igual factor literal ; es decir, a aquellos términos que tienen iguales letras (símbolos literales) e iguales exponentes.

Por ejemplo:

6 a 2 b 3 es término semejante con – 2 a 2 b 3 porque ambos tienen el mismo factor literal (a 2 b 3 )

1/3 x 5 yz es término semejante con x 5 yz porque ambos tienen el mismo factor literal (x 5 yz)

0,3 a 2 c no es término semejante con 4 ac 2 porque los exponentes no son iguales, están al revés.

Reducir términos semejantes significa sumar o restar los coeficientes numéricos en una expresión algebraica, que tengan el mismo factor literal.

Para desarrollar un ejercicio de este tipo, se suman o restan los coeficientes numéricos y se conserva el factor literal.